Contoh Soal Persamaan Kuadrat

Persamaan kuadrat - Image from soalfismat.com

Pengertian Kuadrat dan Persamaan Kuadrat

1. Kuadrat

Kuadrat memiliki definisi yaitu akar kuadrat dari bilangan x sama dengan bilangan r sedemikian sehingga r2 = x, atau, di dalam pengertian lain, bilangan r yang bila dikuadratkan (hasil kali dengan bilangan itu sendiri) sama dengan x.

Baca Dulu : Pusing Mikir Terus? Begini Cara Menghafal Rumus Matematika Dengan Mudah dan Cepat

2. Persamaan Kuadrat

Definisi dari persamaan kuadrat adalah suatu persamaan dari variabel yang mempunyai pangkat tertinggi dua. Bentuk umumnya adalah: Dengan a, b, merupakan koefisien, dan c adalah konstanta, serta a ≠ 0. Penyelesaian atau pemecahan dari sebuah persamaan ini disebut sebagai akar-akar persamaan kuadrat.

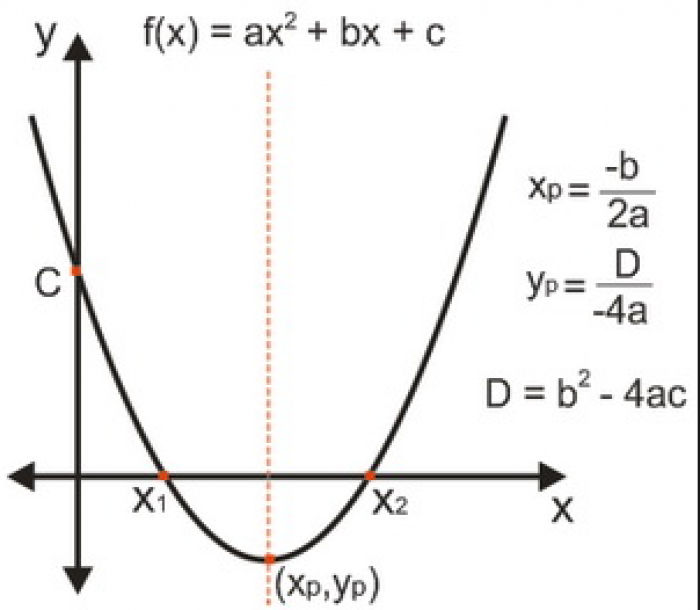
persamaan kuadrat dasar - Image from rumus.co.id

Penyelesaian atau pemecahan dari sebuah persamaan ini disebut sebagai akar-akar persamaan kuadrat. 

Variabel x yang memenuhi persamaan tersebut terdapat nilai yang diambil dari  akar-akar yang dimaksud. Saat nilai tersebut disubstitusikan ke dalam persamaan akan menghasilkan nilai nol.

Akar-akar Persamaan Kuadrat

1. Pemfaktoran

Metode ini mudah digunakan jika akar-akarnya merupakan bilangan rasional. Berikut ini tabel model persamaan kuadrat (PK) dan berbagai cara pemfaktorannya:

akar-akar pemfaktoran - Image from studiobelajar.com

Syarat untuk metode yang satu ini adalah, pertama anda harus mengetahui terlebih dahulu model PK yang akan diselesaikan. Jika syarat tersebut terpenuhi atau PK sudah diketahui, maka pemfaktoran bisa dilakukan dalam bentuk sesuai dengan yang ada di kolom tabel di atas. 

Untuk mengetahui nilai dari p, q, m dan n anda harus memahami cara memfaktorkan suatu bilangan.

Matematika itu asyik, ini contohnya. 
Rumus Matematika ini Bikin Ketawa Ngakak, Kalau Diplesetkan

Persamaan Kuadrat Baru

Diperolehnya rumus yakni dengan cara memanfaatkan rumus abc, sebagai salah satu cara untuk menentukan akar persamaan kuadrat.

Maka didapatkan rumus umum guna mengetahui jumlah dan perkalian dari akar persamaan kuadrat.

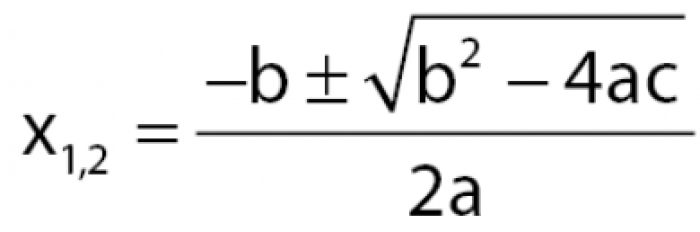
rumus umum - Image from contohsoal.co.id

Berikut ini adalah rumus jumlah dan hasil kali akar persamaan kuadrat.

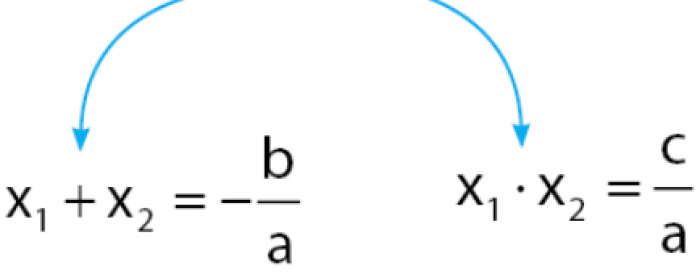
rumus jumlah dan hasil kali - Image from contohsoal.co.id

Persamaan yang dapat digunakan untuk menentukan persamaan kuadrat ialah sebagai berikut.

Persamaan kuadrat awal :

ax² + bx + c = 0

Persamaan kuadrat baru :

x² – ( x¹ + x²) x +x¹ . x² = 0​

Dengan x¹ dan x²merupakan akar-akar dari persamaan kuadrat . Dengan berdasarkan runut, maka langkah-langkah mencari persamaan kuadrat diberikan melalui daftar berikut.

Baca Juga: Cara Cepat Mencari Rumus Deret Geometri + Contoh Soal Lengkap

Langkah-langkah menentukan persamaan kuadrat baru:

Dengan cara menentukan jumlah dari hasil perkalian akar pada persamaan kuadrat awal.
Dengan jumlah hasil perkalian sebuah akar persamaan kuadrat baru yang telah diketahui.
Dengan cara membentuk persamaan kuadrat baru yang sesuai rumus yang telah diberikan di atas.

x² – ( x¹ +x²) + x¹. x² =0

Soal Persamaan Kuadrat

Apabila x1 dan x2 ialah merupakan akar dari persamaan kuadrat x2 – 3x + 5 = 0, maka tentukanlah persamaan kuadrat baru yang akar-akarnya ialah x1 – 3 dan x2 – 3.
Jawab
Agar dapat menyusun persamaan kuadrat baru seperti pada contoh soal di atas, maka dapat menggunakan dua cara yakni dengan rumus jumlah dan hasil kali akar serta dengan rumus khusus. Mari kita bahas satu persatu.

• Menggunakan Rumus Jumlah dan Hasil Kali akar

Persamaan kuadrat x2 – 3x + 5 = 0 memiliki nilai a = 1, b = -3 dan c = 5. Langkah awal yakni tentukanlah terlebih dahulu jumlah dan hasil kali akar persamaan kuadrat lama sebagai berikut.
Jumlah Akar
⇔ x1 + x2 = -b/a
⇔ x1 + x2 = -(-3)/1
⇔ x1 + x2 = 3
Hasil kali Akar
⇔ x1 . x2 = c/a
⇔ x1 . x2 = 5/1
⇔ x1 . x2 = 5
Langkah selanjutnya, kita tentukan jumlah dan hasil kali akar untuk persamaan kuadrat baru yang akar-akarnya x1 – 3 dan x2 – 3 yakni sebagai berikut.
Jumlah Akar
⇔ (x1 – 3) + (x2 – 3) = (x1 + x2) – 6
⇔ (x1 – 3) + (x2 – 3) = 3 – 6
⇔ (x1 – 3) + (x2 – 3) = -3
Hasil kali Akar
⇔ (x1 – 3) . (x2 – 3) = (x1 . x2) – 3x1 – 3x2 + 32
⇔ (x1 – 3) . (x2 – 3) = (x1 . x2) – 3(x1 + x2) + 9
⇔ (x1 – 3) . (x2 – 3) = 5 – 3(3) + 9
⇔ (x1 – 3) . (x2 – 3) = 5
Langkah terakhir kita masukkan nilai jumlah dan hasil kali akar persamaan kuadrat ke dalam rumus umum menyusun PKB yakni sebagai berikut.
⇔x2–(jumlah akar)x+hasil kali akar=0
⇔x2–(-3)x+5=0
⇔ x2+3x+5=0
Maka persamaan kuadrat barunya ialah x2+3x+5=0

• Menggunakan Rumus Khusus

Akar-akar persamaan kuadrat ialah x1 – 3 dan x2 – 3 sehingga akar-akar tersebut berbentuk x1 – n dan x2 – n. Oleh karena itu, kita gunakan rumus nomor #5 yakni sebagai berikut.
a(x+n)2+b(x+n)+c=0
Dari soal kita ketahui nilai a = 1, b = -3, c = 5 dan n = 3. Dengan demikian kita peroleh
⇔ a(x+n)2+b(x+n)+c=0
⇔ 1(x+3)2+(-3)(x+3)+5=0
⇔ x2+6x+9 –3x–9+5=0
⇔ x2+3x+5=0
Jadi persamaan kuadrat barunya ialah x2 + 3x + 5 = 0

Sekian dari kami wajibbaca.com untuk ulasan persamaan kuadrat. Semoga artikel ini dapat memberikan pemahaman tentang persamaan kuadrat.

Persamaan kuadrat itu cukup cukup dikenal oleh siswa secara umum. Bukan tanpa alasan jika kami mengatakan persamaan kuadrat materi umum untuk anak sekolah, apalagi bagi yang sudah duduk di bangku SMA. Karena persamaan kuadrat sudah diperkenalkan kepada para siswa sejak duduk di bangku SMP.

Dikarenakan banyaknya penerapan dari materi persamaan kuadrat ini, mari kita sama-sama coba belajar dari dasarnya. Simak penjelasan di bawah berikut.