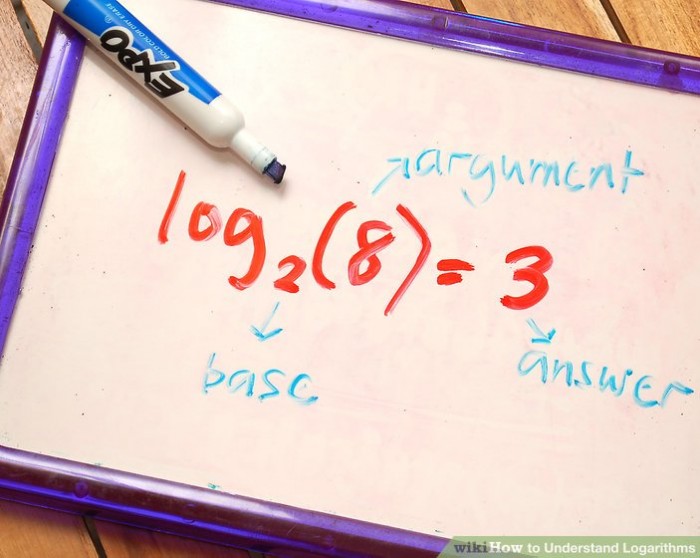
Sifat Sifat Logaritma

Sifat - sifat logaritma - Image from wikihow.com

Pengertian Logaritma

Logaritma adalah invers atau kebalikan dari pemangkatan (eksponen) yang berguna menentukan besar pangkat dari suatu bilangan pokok.

Misalkan, pada sebuah perpangkatan ac= b, maka dapat dinyatakan dalam logaritma sebagai:

Dengan syarat a > 0. Pada penulisan logaritma alog b = c diatas berikut ini keterangannya :

Bilangan (a) disebut sebagai bilangan pokok

Bilangan (b) disebut sebagai bilangan numerus atau disebut juga bilangan yang dicari nilai logaritmanya (b > 0)

Bilangan (c) merupakan hasil dari logaritma tersebut

Jika suatu nilai a sama dengan 10, maka biasanya angka 10 tidak dituliskan sehingga berubah menjadi log b = c.

Dan apabila suatu nilai bilangan pokoknya merupakan bilangan e (bilangan eurel) dengan e = 2,718281828 maka logaritmanya akan ditulis dengan logaritma natural dan pada penulisannya dapat disingkat menjadi ln, misalnya elog b = c menjadi:

Sifat -sifat logaritma - Image from rumus.co.id

Bentuk Umum Logaritma

Bentuk umum dari logaritma ialah sebagai berikut.

Dengan syarat sebagai berikut: b > 0, a > 0 dan a ≠ 1

Keterangan :

a = Bilangannya pokok atau basis logaritma

b = Numerus, yaitu bilangan yang akan dicari nilai dari logaritmanya

x = Hasil logaritma, dapat positif, nol atau bahkan negatif.

Sifat Sifat Logaritma dan Contohnya

1. Sifat sifat logaritma perkalian

Suatu logaritma merupakan hasil penjumlahan dari dua logaritma lain yang nilai kedua numerus-nya merupakan faktor dari nilai numerus awal. Berikut modelnya:

dengan syarat a > 0, a \ne 1, p > 0, q > 0.

2. Perkalian logaritma

Suatu logaritma a dapat dikalikan dengan logaritma b jika nilai numerus logaritma a sama dengan nilai bilangan pokok logaritma b. Hasil perkalian tersebut merupakan logaritma baru dengan nilai bilangan pokok sama dengan logaritma a, dan nilai numerus sama dengan logaritma b. Berikut model sifat logaritma nya:

dengan syarat a > 0, a \ne 1.

3. Sifat logaritma dari pembagian

Suatu logaritma merupakan hasil pengurangan dari dua logaritma lain yang nilai kedua numerus-nya merupakan pecahan atau pembagian dari nilai numerus logaritma awal. Berikut modelnya:

dengan syarat a > 0, a \ne 1, p > 0, q > 0.

4. Sifat logaritma berbanding terbalik

Suatu logaritma berbanding terbalik dengan logaritma lain yang memiliki nilai bilangan pokok dan numerus-nya saling bertukaran. Berikut modelnya:

dengan syarat a > 0, a \ne 1.

5. Logaritma berlawanan tanda

Suatu logaritma berlawanan tanda dengan logaritma yang memiliki numerus-nya merupakan pecahan terbalik dari nilai numerus logaritma awal. Berikut modelnya:

dengan syarat a > 0, a \ne 1, p > 0, q > 0.

6. Sifat logaritma dari perpangkatan

Suatu logaritma dengan nilai numerus-nya merupakan suatu eksponen (pangkat) dapat dijadikan logaritma baru dengan mengeluarkan pangkatnya menjadi bilangan pengali. Berikut modelnya :

dengan syarat a > 0, a \ne 1, b > 0

7. Perpangkatan bilangan pokok logaritma

Suatu logaritma dengan nilai bilangan pokoknya merupakan suatu eksponen (pangkat) dapat dijadikan logaritma baru dengan mengeluarkan pangkatnya menjadi bilangan pembagi. Berikut modelnya:

dengan syarat a > 0, a \ne 1.

8. Bilangan pokok logaritma sebanding dengan perpangkatan numerus

Suatu logaritma dengan nilai numerus-nya merupakan suatu eksponen (pangkat) dari nilai bilangan pokoknya memiliki hasil yang sama dengan nilai pangkat numerus tersebut. Berikut model sifat logaritma nya:

dengan syarat a > 0 dan a \ne 1.

9. Perpangkatan logaritma

Suatu bilangan yang memiliki pangkat berbentuk logaritma, hasil pangkatnya adalah nilai numerus dari logaritma tersebut. Berikut modelnya:

dengan syarat a > 0, a \ne 1, m > 0.

10. Mengubah basis logaritma

Suatu logaritma dapat dipecah menjadi perbandingan dua logaritma sebagai berikut:

dengan syarat a > 0, a \ne 1, p > 0, q > 0

Apa sih logaritma itu? Apa bedanya dengan algoritma? Berikut ini wajibbaca.com uraikan pengertian logaritma dan sifat-sifat logaritma.